大問2(1)解答例二つ

さて、解説です。　(1)はさらっと。

問題はこちら。

大問２(1)　(解答例.1)

$$g(t)=\frac{1}{t}とする。　(t>0)$$

\(g'(t)<0\)より、\(g(t)\)は狭義単調減少関数。 これと面積の関係より（図１参考）

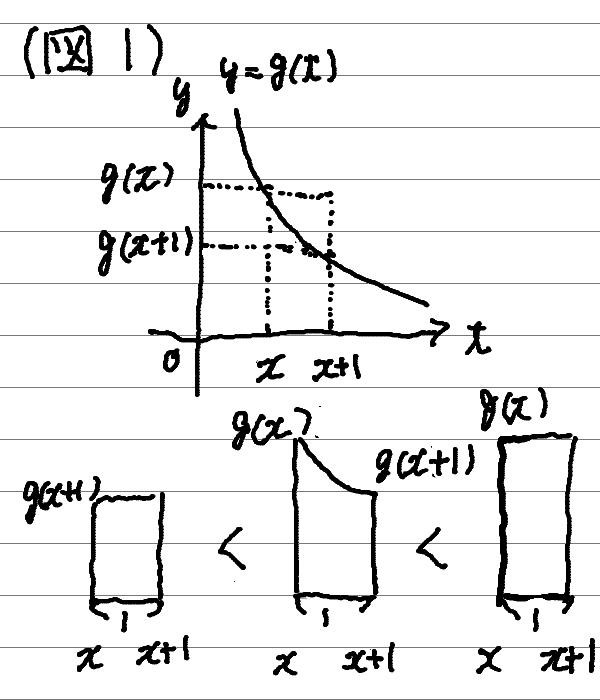
$$\frac{1}{x+1}<\int_x^{x+1} \frac{1}{t}dt<\frac{1}{x}$$

$$\frac{1}{x+1}<log|x+1|-log|x|<\frac{1}{x}$$

\(x>0\)とあわせて

$$\frac{100}{x+1}<100\{log(x+1)-log(x)\}<\frac{100}{x}$$

$$ ∴　\frac{100}{x+1}<f(x+1)-f(x)<\frac{100}{x}\ 　　■$$

つづいて

大問２(1)　(解答例.2)

$$g(t)=\frac{1}{t}とする。　(t>0)$$

\(y=g(t)\)は閉区間\([x,x+1]\)で連続、開区間\(（x,x+1）\)で微分可能。\(（x>0）\)

よって平均値の定理により

$$\frac{log(x+1)-logx}{x+1-x}=\frac{1}{c}$$

即ち、

$$log(x+1)-logx=\frac{1}{c}　・・・①$$

\((x<c<x+1)\)を満たす\(c\)が存在する。

$$また、y=\frac{1}{n}は単調減少関数より、$$

$$\frac{1}{x+1}<\frac{1}{c}<\frac{1}{x}　・・・②$$

①,②より

$$\frac{100}{x+1}<100\{log(x+1)-log(x)\}<\frac{100}{x}　$$

　$$　∴　\frac{100}{x+1}<f(x+1)-f(x)<\frac{100}{x}　
　■$$

この問題に関しては、思いつくか思いつかないかの差だけです。

時間にして10分程度で完了ってかんじですかね。

ま、(2)を解くための布石です。

問題的には次回以降面白くなりますよ。